NAGphormer: A Tokenized Graph Transformer for Node Classificationn in Large Graphs

NAGphormer: A Tokenized Graph Transformer for Node Classificationn in Large Graphs[ICLR2023]

用于大图中节点分类的标记化图Transformer

• 研究背景

Transformer在其他的图挖掘任务中都表现的很好，但是现有的Graph Transformer都是将节点视为独立的token，并构建由所有节点token组成的单个长序列来训练Transformer模型，由于自注意计算的节点数量的二次复杂性，导致它很难扩展到大型图（Large Graphs）。

也就是说如果只是将每一个节点都单独视为独立的token，在大图中，送进Transformer的序列就会很长。因此想要解决这个问题

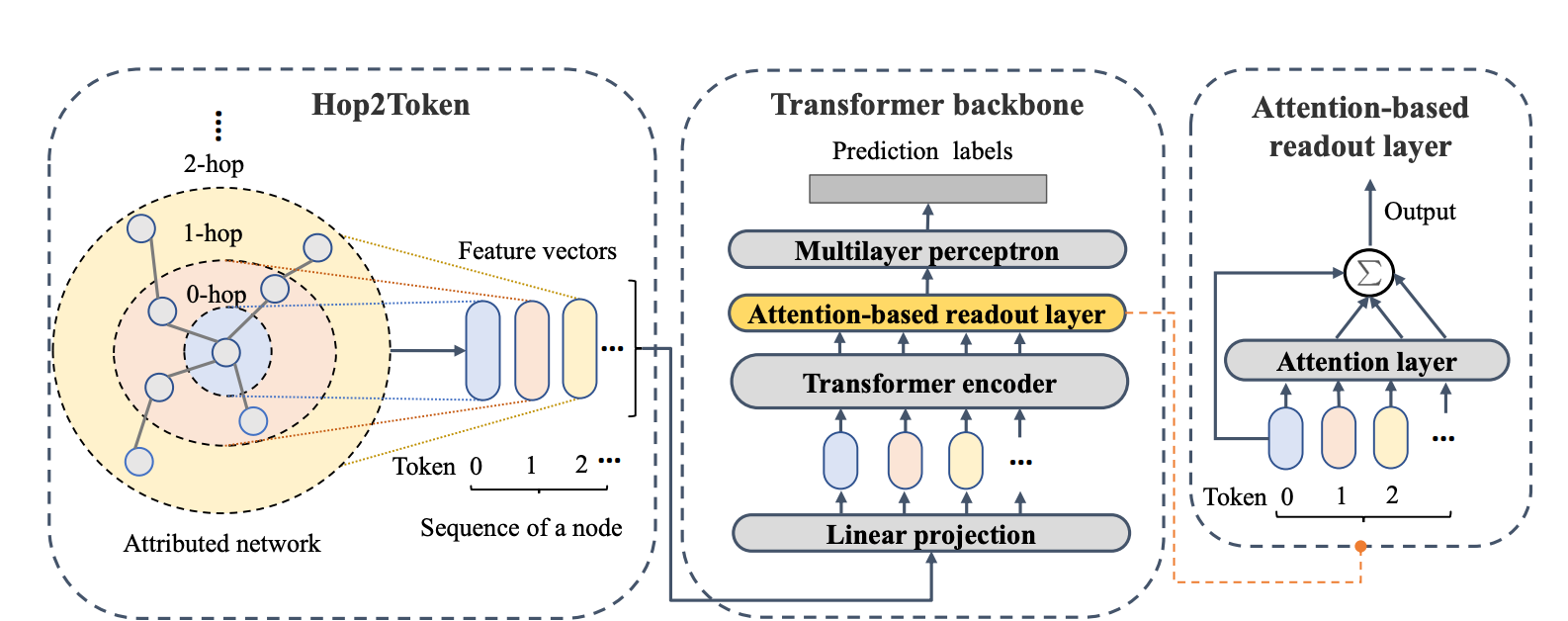
• 如何解决的？

  ①提出Hop2Token。Hop2Token将节点的邻域进行聚合。对于每个节点，Hop2Token将来自不同跳的邻域特征聚合为不同的表示，从而得到一个token vector序列作为一个输入。通过这种方式，NAGphormer可以以小批量的方式进行训练，从而可以扩展到大型图。（对于一个图来说，聚合k跳邻居的k是超参数，所以对于任何一个节点得到的邻域token vector的长度都是k。）

  ②通过Hop2Token我们就可以得到$\text{X}_G$ ，可以将X_G视为一个序列$S = (\text{X}_0, \text{X}_1, …, \text{X}_K)$，其中X_k表示k-hop邻居矩阵，也就是X0 = X, X1 = AX, X2 = A(AX)，以此类推。 对于序列$S_v = (\text{x}_v^0, \text{x}_v^1,…, \text{x}_v^K)$ 送进Transformer前，在经过一个learnable 线性变换$\text{E}$得到$Z_v^{(0)} = [\text{x}_v^0\text{E};\text{x}_v^1\text{E}; …;\text{x}_v^K\text{E}]$。把Z送进Transformer，相当于对于每一个节点，计算其本身(0-hop)与1-hop，2-hop ,…, k-hop邻域的注意力，并得到每一跳邻域的表征，然后再将每一跳邻域的表征通过一个Attention-based READOUT（在GNNs中常常使用的READOUT是sum,mean之类，然而在邻域这种条件下，sum&mean就忽略了不同邻居的重要性是不一样的，作者受GAT启发，就搞了一个Attention-based READOUT，可以单独又计算0-hop和不同hop邻域的注意力，可以学到不同的重要性），再紧接一个MLP，就得到该节点的prediciton label。

  该方法的时间复杂度是$O(n(K+1)^2d)$，对于large Graph，K和d是提前设定的，也就是节点数n的线性复杂度。空间复杂度$O(b(K+1)^2 + b(K+1)d + d^2L)$，第二项是多出来的一层Attention-based READOUT的参数引入的，第三项是MLP的参数所引入的。

• 优点和缺点

  优：①可以在大图上使用。将每一个node的固定K跳邻居变成一个K维的序列送入Transformer，而不是直接将所有node变成一个序列送入Transformer，避免了送入Transformer的序列很长，同时可以提前计算k-hop的X，同时还可以小批量送进网络进行处理。②时间复杂度$O(n(K+1)^2d)$是n的线性复杂度。

  缺点：空间复杂度高，除了Transformer backbone的开销，引入的Attention-based READOUT也多了参数，最后的MLP也新的参数，可能内存占用比较大。另外，没有用OGB数据集做实验，我认为应该加入OGB节点分类相关数据集的实验。