A Generalization of Transformer Networks to Graphs

A Generalization of Transformer Networks to Graphs (GT) [AAAI 2021]

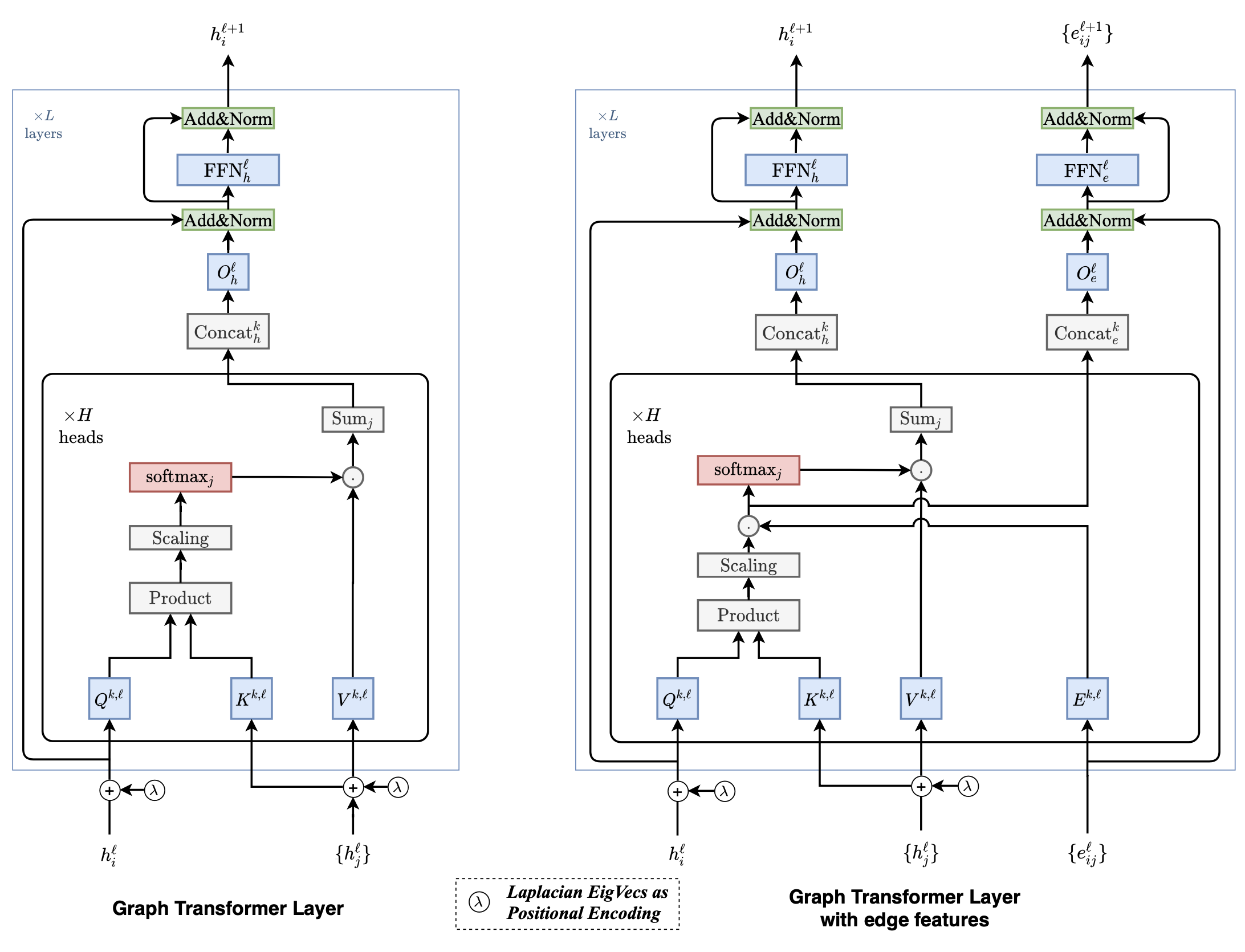
• 研究背景、现有的方法存在什么问题？

最初的Transformer是为NLP设计的，其中的self-attention会计算一个句子中两两word之间的注意力。在这种架构下，由于Graph上的拓扑结构信息很重要，如果拓扑信息没有编码到节点表征中时，直接两两计算节点间的注意力往往会表现的很差。

• 研究的是在什么场景下的什么问题？

如文章标题一样，本文并未限定具体的任务场景。本文做了Graph Regression、Node Classification两大类任务。

• 如何解决这个问题的？为什么要这么解决（动机Motivation）

（也就是说我们不应该计算所有节点之间的两两注意力，而是更应该关注节点的邻居）。除此以外，想要直接在图上应用原始Transformer里的PE是困难的，因为在原始Transformer(也就是Attention is All You Need)里的PE可以保证每个单词具有唯一的位置表示，但是图上节点间的连接具有对称性，所以要设计能够得到节点唯一位置表示的PE是困难的（所以应该换一种PE）。

① attention机制只关注节点的邻居 ② 用拉普拉斯特征向量来表示位置编码PE ③ 用batch norm代替layer norm —>训练的更快、泛化性更强 ④ 并将提出的模型扩展到了边表征上，可以兼容节点表征和边表征（边表征在化学分子预测、知识图谱的实体预测上很重要）

• 好不好？新方法有什么问题？

① 在Graph上使用局部自注意力机制是自然的，因为节点应该更多关心与其相连的邻居，而并非全局的所有节点。相较于global, 使用Local自注意力机制减少了计算量，能更有效的捕捉节点之间的局部依赖关系，且解释起来也是很自然的。但是使用local，在全局性的任务上会有一定的弱化，难以从整体理解图的结构和语义，也难以捕获长距离的依赖。

②用Laplacian 特征向量来表示PE的理由是什么？在图信号处理中，拉普拉斯矩阵的特征向量（也叫谱特征向量）就是用来表示节点的位置信息的，提供了节点在图中的相对位置和连接关系。通过使用拉普拉斯矩阵的特征向量，可以将节点映射到低维空间，从而实现图的降维和表示。所以使用拉普拉斯矩阵的特征向量能保证每个节点的PE都是唯一的吗？

③batch norm和layer norm。BN可以并行、LN只能顺序执行。

④引入egde feature

特别的地方：

• 使用节点的最小的k个non-trival 特征向量（非平凡特征向量就是对应于非零特征值的特征向量）作为该节点的位置编码。
• 节点表征h + 位置编码λ 之后再送入Transformer
• 不需要计算两两节点间的注意力，只需要计算该节点和其邻居之间的注意力
• 预先计算数据集中所有图的拉普拉斯矩阵的特征向量
• 还能融合edge feature