GraphPrompt: Unifying Pre-Training and Downstream Tasks for Graph Neural Networks
Published:
GraphPrompt: Unifying Pre-Training and Downstream Tasks for Graph Neural Networks [WWW2023]
Pre-training task: link prediciton
Downstream tasks: 节点分类(节点级)、图分类(图级)
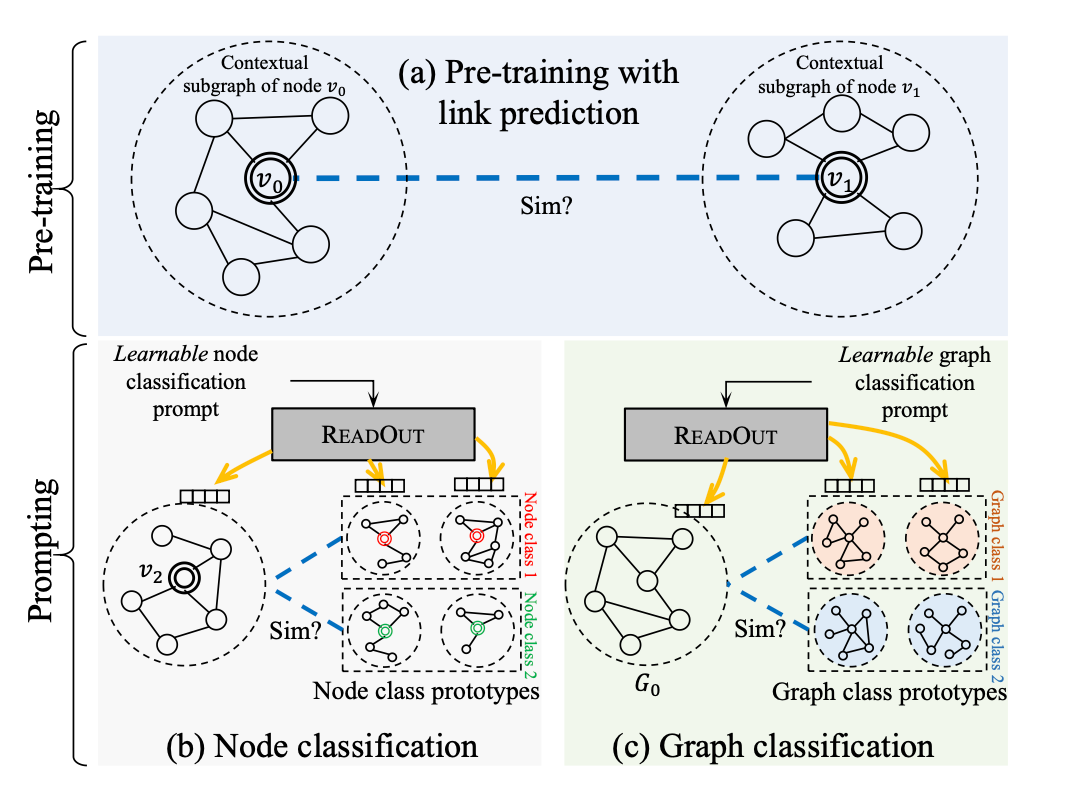
要实现这样一个统一的框架,需要将上游预训练的链路预测问题、下游的节点分类问题和图分类问题转化为统一的template,本文就是将这些不同的上下游任务转换成基于子图相似性的相同训练模板。
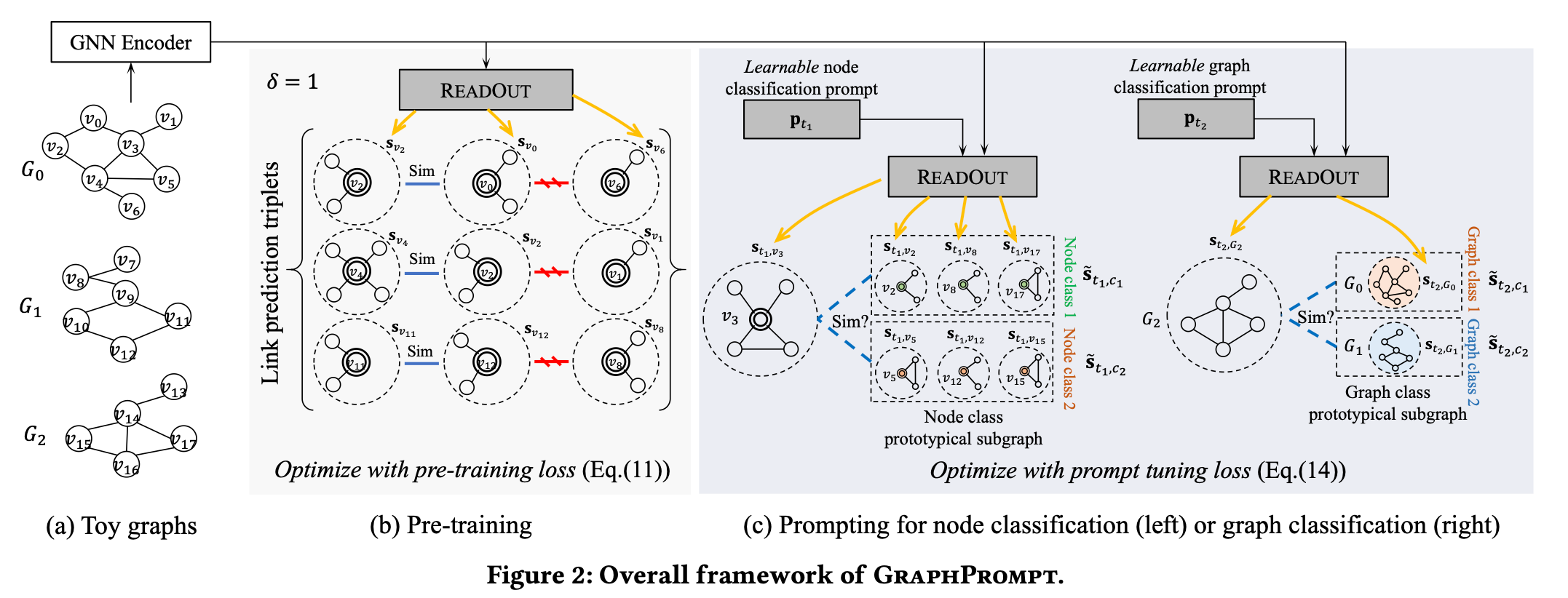
那么如何将预训练的link prediction转化为基于子图相似性模板呢?对于一个图G=(V,E),和一个三元组(v,a,b), (v,a)∈ E且(v,b)∉E,三个节点v,a,b对应向量表征$s_v, s_a,s_b$ ,则我们应该有 $sim(s_v,s_a) > sim(s_v,s_b)$ ,直观地说v应更类似于相连接的节点a 而不是另一个未连接的节点b。 (节点v对应的向量表征$s_v$在这里并不是其自身的表征,而是其对应的上下文子图$S_v$的表征,而$S_v$ 是由节点v的$\delta$跳之内的节点和边构成,$\delta$是预先设定的threshold)。
那么如何将下游节点分类转化为子图相似性学习(Subgraph similarity learning)模板(template)呢?定义一个节点类原型子图(node class prototypical subgraph)由$\tilde{s_c}$表示, $ \tilde{s_c} = \frac{1}{k} \sum_{(v_i,l_i)\in D, l_i=c}s_{v_i}$ 它被构造为给定类中标记节点的上下文子图的平均表示,然后对于一个不在labeled set D里的节点$v_j$, 其类标签(class label) $l_j$ 应为 $l_j = arg max_{c\in C}sim(s_{v_j}, \tilde{s_c})$ 。直观地说,一个节点应该属于其原型子图与该节点的上下文子图最相似的类。也就是说分别计算节点$v_j$ 和每一个类c的原型子图之间的相似度,相似度最大的那个类c即为节点$v_j$属于的类。
那么如何将下游图级别分类转化为子图相似性学习模板呢?定义一个图类别原型子图(graph class prototypical subgraph)
同样由(sub)graphs的平均嵌入向量来表示,$ \tilde{s_c} = \frac{1}{k} \sum_{(G_i,L_i)\in D, L_i=c}s_{G_i}$ 。对于一个不在labeled set D里的图$G_j$,其类标签应为$L_j = arg max_{c\in C}sim(s_{G_j}, \tilde{s_c})$。直观地说,图应该属于其原型子图与其自身最相似的类。
===> 怎么获取subgraph $S_x$对应的subgraph embedding vector $s_x$呢?学出来。
===> 怎么学出来?
首先通过GNN得到节点表征$h_v$,计算$s_x$的标准方法是使用READOUT操作,也就是将子图$S_x$里的节点表征进行聚合:
$s_x = READOUT({h_v:v \in V(S_x)})$ ,我们知道READOUT的方法有很多,本文使用sum pooling来实现。
定义好了统一的上下游训练模板,怎么训练呢?
预训练阶段
给定一个图G上的节点v, 我们随机从v的邻居抽取一个正节点a,从不与v相连的一个负节点b, 形成三元组(𝑣, 𝑎, 𝑏). 我们的目标是增加上下文子图之间的相似性𝑆𝑣 和𝑆𝑎, 同时降低𝑆𝑣 和𝑆𝑏 . 更一般地,在一组无标签图G上,我们从每个图中采样多个三元组,以构建整体训练集$T_{pre}$。定义如下预训练损失:
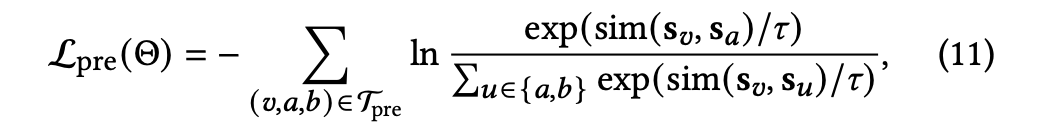
也即$S_v与S_a$损失越小。$\Theta$代表GNN模型权重。
Prompt Design
预训练与下游任务的统一使得知识迁移更有效,但区分不同的下游任务依然很重要。在子图相似性学习的相同任务模板下,READOUT操作(用于生成子图)可以针对不同的下游任务进行不同的“提示”。节点分类更加关注与目标节点在局部上更相关的特征。相比之下,图分类倾向于关注与图类相关的特征。更重要的是,给定任务中不同的实例或类集,重要的特征也会有所不同。具体来说对于特定的任务t,定义对应的可学习的prompt向量$p_t$为一种按维度的重新加权,以提取与任务t最相关的先验知识,则prompt-assisted READOUT定义为:$s_{t,x} = READOUT({p_t\odot h_v: v \in V(S_v)})$。当然,prompt的设计也可以是其他的形式,本文采用的即是上述形式。(除了使用这种reweighting的prompt,还可以有对$h_v$进行线性变换(Linear Transformation),也可以是更加复杂的prompt,如Attention layer)
Prompt tuning
为了优化the learnable prompt,也即prompt tuning,我们使用prompt-assisted的任务特定子图表示,基于子图相似性的公共模板来制定损失:
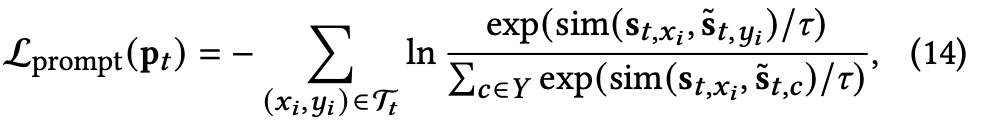
参数变成了可学习的Prompt Pt,而不再需要GNN weight,因为预训练时的GNN weight在下游任务训练时是frozen(因为fine-tuning是非必要的了,用learnable prompt替代)
Experiments
详见paper
